Si tomas un pedazo de papel, ese papel tendrá dos caras, ¿verdad? Si quisieras, podrías pintarlo de azul por una cara y de rojo por la otra, ¿no? E incluso si enrollas el papel como un tubo, seguirá teniendo dos caras, una interior y otra exterior.
Pero ¿ podrías tener un pedazo de papel con sólo una cara? Veamos. Toma un pedazo de papel y corta una tira larga y estrecha. Con un lápiz pon una A en el extremo izquierdo de la tira y una B en el extremo derecho.

Ahora, da la vuelta a la tira, conservando la B a tu derecha. Junta los dos extremos. Da media vuelta al extremo B y coloca la B sobre la A. Pega los dos extremos con cinta adhesiva transparente y refuerza con ella ambas caras. Ya tienes un lazo con media vuelta.
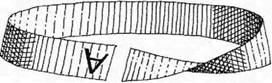
El lazo parece tener dos caras, ¿verdad que sí? Si tuvieras un lazo gigante, tú y un amigo podríais empezar a colorear cada uno una de las caras, una en rojo y otra en azul.
Pero si lo intentaseis, quedaríais sorprendidos al ver que los colores llegan a encontrarse.
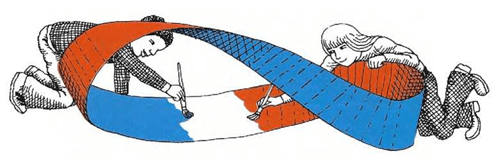
Porque, de hecho, este tipo de lazo no tiene más que una cara. Podrás comprobarlo coloreando de rojo tu pequeño lazo.
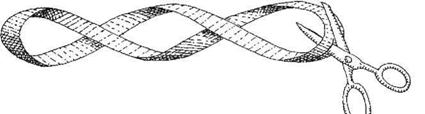
Este tipo de lazo con vuelta se denomina banda de Mobius, apellido del científico que la inventó. Y es un juguete extraño y casi “mágico”, con el que se pueden hacer algunas cosas sorprendentes. Por ejemplo, ¿qué crees que ocurriría si tuvieses que cortar una tira de Mobius en toda su longitud por el medio? ¿Crees que obtendrías dos lazos? ¡Ciertamente
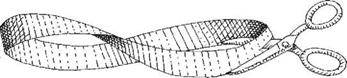
nol Cuando hubieses acabado de cortarla por la “mitad” verías que seguías teniendo una sola tira, sólo que dos veces más larga.
Proclamó un eminente matemático:
“La banda de Mobius tiene un solo lado”.
Te carcajearás como un lunático si la cortas a lo largo. ¡Fantástico!
No la has partido, pese a haberla cortado.
¿Qué crees que ocurrirá si cortas nuevamente ese lazo a lo largo ? Inténtalo y verás.