Adaptación de la obra Pianilandia, de A. Cuadrado.
Llamaré a mi país Pianilandia, no porque nosotros lo conozcamos por este nombre, sino para que puedas hacerte una idea de cómo es. Has de saber, en primer lugar, que en mi país no existe ni una figura sólida. Como bien te consta, una figura sólida o tridimensional tiene longitud, anchura y altura. Pero en Pianilandia todo es plano. Es decir, que no hay más que dos dimensiones, longitud y anchura.
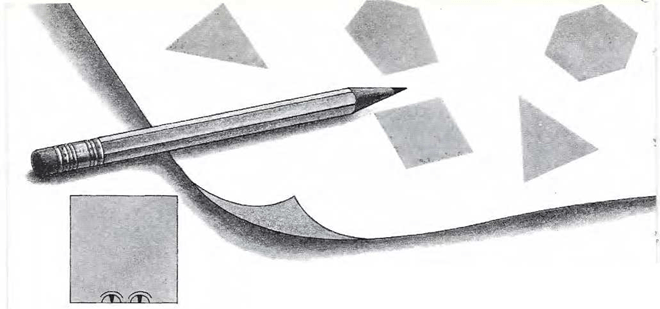
Imagina una enorme hoja de papel por la que se mueven libremente líneas rectas, triángulos, cuadrados, pentágonos, hexágonos y otras figuras; esto te dará una idea bastante correcta del aspecto de mi país y de mis compatriotas. Quizá pienses que se puede, a simple vista, saber cuáles son los triángulos, cuáles los cuadrados y cuáles las demás figuras. Pero no es así. No se puede saber cuál es cuál. No se reconocen más que las líneas rectas. Déjame que te diga por qué.
Coloca una moneda encima de la mesa. Ahora, inclínate sobre la mesa y mira la

moneda de arriba abajo. Te parecerá un círculo. Pero retrocede hasta el borde de la mesa y baja la cabeza. Cuando tengas los ojos a la misma altura del borde de la mesa (como si fueses uno de los habitantes de nuestro país) la moneda ya no te parecerá un círculo. Creerás que se ha convertido en una línea recta.
Lo mismo ocurrirá si tomas un trozo de cartulina y recortas un ti ángulo, un cuadrado o cualquier otra figura. Pon la figura encima de la mesa y mírala desde el borde. Verás únicamente una línea recta.
Pues bien, eso es exactamente lo que vemos en mi país cuando nos encontramos a un amigo. Según se va acercando más y más a nosotros, la línea se hace más grande y más nítida. Cuando nuestro amigo se aleja, la línea se hace más pequeña y apagada. Puede que nuestro amigo sea un triángulo, un cuadrado, un pentágono, un hexágono o cualquier otra figura, pero lo único que vemos es una línea recta.
Quizá te preguntes cómo podemos distinguir un amigo de otro. Te lo explicaré en un momento. Pero antes, déjame que te diga qué clase de gente hay en Planilandia.
Nuestros soldados son líneas rectas. En seguida te diré algo más sobre ellos.
Todos nuestros granjeros son triángulos isósceles, con dos lados iguales, cada uno de los cuales mide 27 centímetros. El tercer lado
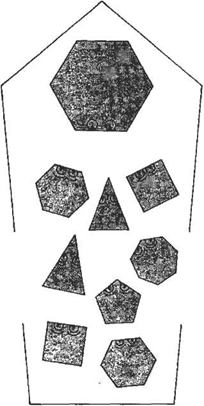
es bastante corto; a veces no mide más de 12 milímetros. Esto hace que los dos lados largos formen un ángulo muy agudo, útilísimo para arar.
Nuestros comerciantes y tenderos, de los que tenemos muchos, son triángulos equiláteros.
La mayor parte de nuestros mejores médicos y abogados son cuadrados, como yo mismo. Y unos cuantos, que han llegado a lo más alto en sus profesiones, son figuras de cinco lados, o sea, pentágonos. Hay distintos grados de profesores, comenzando por los que son figuras de seis lados, es decir, hexágonos, hasta los que son figuras de muchos más lados. Finalmente, tenemos los filósofos, que son nuestros ciudadanos más sabios. Tienen tantos lados, y los lados son tan pequeños, que no pueden distinguirse de un círculo.
Hay muchos peligros en Planilandia, al igual que en vuestro mundo. El mayor peligro son nuestras propias figuras. Hemos de tener muchísimo cuidado para no toparnos los unos con los otros. Los que tienen figuras puntiagudas pueden hacer daño fácilmente a otras personas. Por esta razón son tan peligrosos nuestros triángulos campesinos.
Siendo esto así, pronto habrás adivinado que nuestros soldados son aún más peligrosos. Si un granjero es como una flecha, un soldado es como una aguja, ya que el soldado está formado por puntos (como sabes, una línea está enteramente formada por puntos). Si añades a esto la facultad que tienen los soldados de volverse casi invisibles, advertirás que los militares de nuestro país no pueden tomarse a broma.
Quizá te preguntes cómo pueden hacerse invisibles nuestros soldados. Te lo explicaré.
Pon una aguja encima de la mesa. Ahora,
mírala de lado desde el borde de la mesa.
Verás toda su longitud. Pero mírala de frente, y no verás más que un punto. Se ha vuelto prácticamente invisible. Esto es lo que pasa con nuestros soldados. Cuando están de lado, los vemos como una línea recta. Cuando están frente a nosotros no vemos más que un punto que brilla. Pero cuando nos dan la espalda, son un mínimo punto casi imposible de distinguir.
¿Entiendes por qué son tan peligrosos nuestros soldados? Puedes llevarte un buen coscorrón si topas con un triángulo comerciante, o resultar gravemente herido si colisionas con un triángulo granjero. Pero topar con un soldado puede ser dolorosísimo.
Cuando el soldado no es más que un punto borroso, resulta muy difícil, incluso para el más cauto, evitar la colisión.
Por esta razón, nuestros soldados han de tener mucho cuidado. En la calle, parados o andando, deben mover constantemente la espalda de lado a lado para que quien vaya detrás pueda verles.
Afortunados vosotros, los que vivís en un mundo de tres dimensiones: tenéis la sombra y la luz. Disfrutáis de muchos colores. Podéis ver un ángulo y la forma completa de un círculo.
Pero en Planilandia no tenemos estas bendiciones. ¿ Cómo puedo, pues, hacerte entender la dificultad que tenemos para reconocemos los unos a los otros ?
El primer medio de reconocimiento es el sentido del oído. Nuestro oído es más fino y está mucho más desarrollado que el vuestro.
Nos permite no sólo reconocer las voces de nuestros amigos, sino incluso percibir la diferencia entre figuras, al menos el triángulo, el cuadrado y el pentágono.




Pero el tacto es el mejor medio para reconocer a otro habitante de mi país. El tacto es para nosotros lo que las presentaciones para vosotros. En Planilandia la gente se presenta así: “Permítame que le toque, y toque usted también a mi buen amigo el señor Fulano de Tal.”
Sin embargo, no creas que nuestro tacto es tan lento y difícil como puede ser en vosotros.
La mucha práctica y los entrenamientos, que empiezan en la escuela y duran toda la vida, nos permiten distinguir rápidamente un triángulo equilátero de un cuadrado o un pentágono.
Generalmente, no hace falta tocar más que un ángulo para saber la forma de una persona, a menos que ésta pertenezca a la clase alta de las figuras. Entonces es mucho más difícil. Se sabe que incluso nuestros profesores de la universidad han confundido un polígono de diez lados con uno de doce. Y no creo que exista ningún doctor en ciencias en Planilandia que pueda reconocer a la primera, sólo tocando uno de sus ángulos, la diferencia entre una figura de veinte lados y otra de veinticuatro. Muchos, sin embargo, prefieren un tercer método de reconocimiento: el sentido de la vísta.
La existencia de este poder, del que disponen todas las clases, se debe a la niebla, presente en todas paites durante la mayor parte del año, excepto en las zonas más calurosas de Planilandia. Para vosotros, la niebla es mala, pues os oculta el paisaje, os hace sentir tristes y daña vuestra salud. Pero para nosotros, constituye una bendición, y es casi tan importante como el propio aire.
Si no hubiese niebla en nuestro país, todos nuestros amigos tendrían exactamente la misma apariencia que la línea recta. Pero allí donde hay una buena cantidad de niebla, cualquier objeto que esté algo más alejado que otro, ya está más borroso que el más cercano. Así pues, examinando cuidadosamente el brillo o lo apagado de las cosas, podemos saber la forma exacta de un objeto.
Por ejemplo, supongamos que veo a dos personas acercándose. Digamos que una es un comerciante (un triángulo equilátero) y la otra un médico (un pentágono). Ambos parecen una línea recta: entonces, ¿cómo puedo distinguir a uno del otro ? Si miras el dibujo, creo que lo comprenderás.
En el caso del comerciante, veo una línea recta, naturalmente. El centro de esta línea, la parte más cercana a mí, es muy brillante. Pero los lados desaparecen rápidamente en la niebla. Entonces veo que la línea retrocede oblicua y bastante afilada desde el centro.
Por otro lado, el médico tiene un aspecto ligeramente distinto. Del comerciante tan sólo percibía una línea recta con un centro muy brillante. La línea del médico también desaparece por los lados en la niebla. Pero no tan rápidamente como la del comerciante. Así pues, puedo ver inmediatamente que la línea del médico no retrocede de manera tan oblicua como la del comerciante. Debido a esta ligera diferencia, sé que una de las formas es un triángulo equilátero y la otra un pentágono.
Pero ya está bien de explicar cómo nos reconocemos. Déjame decirte unas palabras sobre nuestro clima y nuestras casas.
Al igual que vosotros, tenemos cuatro direcciones: Norte, Sur, Este y Oeste. Pero, como no tenemos Sol —ni ningún otro cuerpo . celeste—, en Planilandia es imposible decir cuál es el Norte, como hacéis vosotros. Sin embargo, tenemos nuestro propio método.
Debido a una ley de la naturaleza, en Planilandia hay una atracción constante del Sur. Esta fuerza es suficiente para hacer el papel de brújula en la mayor parte de nuestro país. Además, la lluvia, que cae a horas fijas cada día, siempre viene del Norte. Y, como comprenderás, es una buena ayuda adicional.
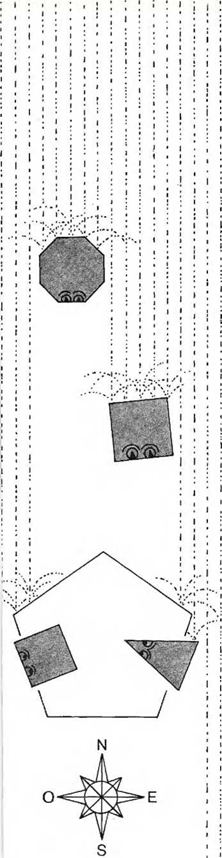
En las ciudades, nos orientamos por medio de las casas, pues todas ellas están construidas con el tejado apuntando al Norte, para resguardarnos de la lluvia.
Sin embargo, en nuestras regiones más septentrionales apenas se siente la atracción del Sur. Por eso, algunas veces en que me encontraba paseando por alguna zona donde no había casas para guiarme, he tenido que esperar varias horas hasta que ha llegado la lluvia. Sólo entonces he podido asegurarme de en qué dirección iba. Nuestras casas son muy confortables y muy adecuadas a nuestro clima y nuestro modo de vida. La construcción más común en Planilandia tiene forma de pentágono; es decir, cinco lados, como ves en el dibujo.
Los dos lados del Norte forman el tejado y generalmente no tienen puertas. La puerta de entrada está en el lado del Este. Al Oeste hay otra puerta para salir. Así podemos entrar y salir sin chocar unos contra otros y hacernos daño. El lado Sur, es decir, el suelo, generalmente no tiene puerta.
Las casas cuadradas o triangulares no están permitidas, por una razón: los ángulos de un cuadrado (y aún más los de un triángulo) son mucho más puntiagudos que los ángulos de un pentágono. Las líneas de las casas y las de los demás objetos son más apagadas que las líneas de los hombres y las mujeres. Así pues, existe el peligro de que los ángulos de una casa cuadrada o triangular puedan causar daño grave a algún caminante distraído que tropiece corriendo con ellas.
Ya en el siglo once de nuestra era, las casas triangulares estaban prohibidas por la ley. Las únicas excepciones eran los fuertes y otros edificios similares, cuyos bordes afilados tenían una función útil. En aquella época, aún se permitían las casas cuadradas. Pero unos tres siglos después, los legisladores decidieron (por razones de seguridad pública) que en las ciudades con una población de más de 10.000 habitantes, sólo se permitieran casas cuyo ángulo más pequeño fuese el del pentágono.
Sólo de vez en cuando, en remotas comarcas rurales, aún se puede ver alguna casa cuadrada.
Nuestras casas no tienen ventanas, dado que la luz nos llega por dentro y por fuera, de día y de noche, y a todas horas y en todos los sitios. Pero no sabemos de dónde viene la luz. Antiguamente, nuestros sabios trataron de descubrir la causa de la luz, pero muchos se volvieron locos intentando resolver el problema y pronto se nos llenaron los manicomios.
Sólo yo —¡cielos!, sólo yo en Planilandia— tengo la solución verdadera a este misterioso problema. Pero no puedo llevar mi conocimiento a la comprensión de uno solo de mis compatriotas. Se burlan de mí, de mí, el único que sabe la verdad: la luz nos llega de vuestro extraño mundo de tres dimensiones.

Construye tu propio tetraedro calcando este dibujo. Sigue las instrucciones que encontrarás en estas páginas.

